Fall couldn’t be more complete with this salad of crisp apple slices, arugula, cranberries, and cashew drizzled with a tart and sweet Apple Vinaigrette…
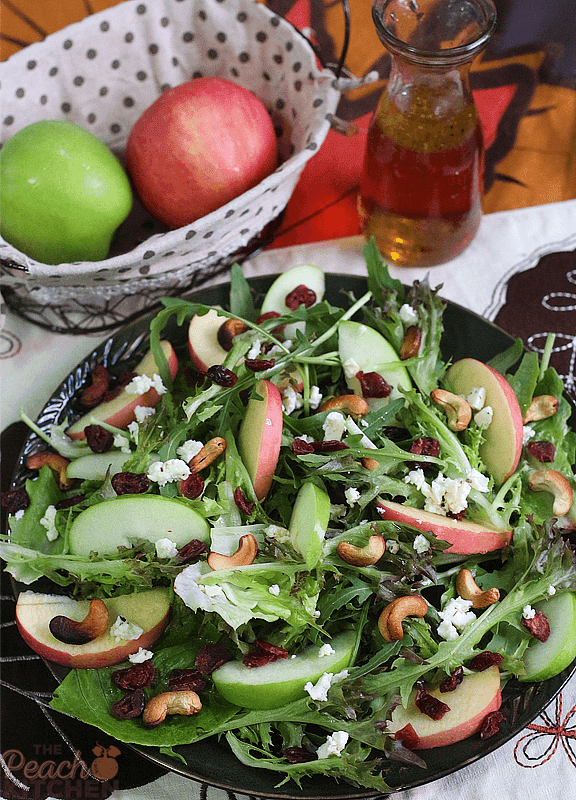
Salads are back! Hopefully, I can make them stay for good.
I’ve been adding salads to our daily meal to keep it healthier and to inspire my daughter to fall in love with salads once again.
I wasn’t ready yet to let go of Fall yet but the holidays was able to sneak in without me knowing so to bid Fall adieu, here’s an Autumn salad made with ingredients that are in season — crisp apples. Oh, and we have lots of cashews at home courtesy of relatives from Palawan. So this is practically begging to be made. So good with this Apple Vinaigrette.
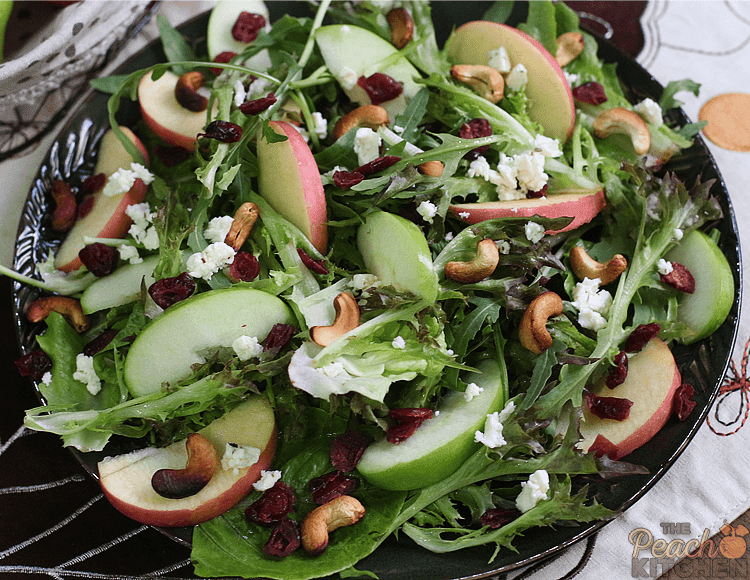
It’s still crazy here at the Adarne household. My mind is in a merry-go-round juggling work, mommy duties, household chores, and more work.
To add to all of the “excitement” everybody’s been coming down with something! The whole family has colds and the little ones have coughs to go with their colds. peeanutbutter♥ and I are worried sick with our little one. It’s hard to see her coughing at night when asleep. If only I can somehow absorb her coughs and colds, I will.
We were at the doctors yesterday and got prescriptions. I’m hoping everyone will feel better soon in a couple of days. We just have to. We weren’t even able to celebrate Twinkle’s 5th month with her Supergirl Party yet because we’re all sick. *sniff* .. And she’ll be six months old on Christmas Day.
In addition to that are a million more things I just couldn’t possibly divulge here.

Crossing my fingers I can get through this holiday unscathed.
PrintApple Cranberry Cashew Salad
- Author: Peachy Adarne
Ingredients
- 4 cups of greens (I used a mix of arugula, romaine, and french red frissee)
- 1 red apple (I used fuji apple)
- 1 green apple
- 1/2 cup cashew nuts
- 1/4 cup dried cranberries
- 1/4 cup crumbled feta cheese
- Apple Vinaigrette (click for the recipe)
Instructions
- Core the apple and sliced thinly.
- Combine lettuce, apple, cashew, dried cranberries and crumbled feta cheese in a large bowl.
- Toss to mix.
- Drizzle with Apple Vinaigrette just before serving and toss again.
- Serve as a side to meat or fish.























89 Responses
wow Peach, that’s my kind of meal…both salad and baked salmon look so GOOD!!
Thanks so much Angie!
I don’t eat salad but I love baked salmon. An easy dish that you can prepare in several minutes. 🙂
The salad looks really good! The mixed of different greens and the sweetenest of fruits is perfect pair. The baked salmon looks delicious!:) Thanks for the recipe! Will try this one soon.
you’re welcome melgie! Hope you like it.
Your food posts keep me encouraging to work in the kitchen. =) I love preparing meals and making them look special. Your posts give me an idea. =)
Thanks Gilian!
I really like this and it’s perfect timing too because my hubbys on a diet! Love the apples in this, and great choice pairing this with a baked salmon and asparagus!
★★★★★
Thanks katriza!
I love salads with apples. Saya saya!
heehee. Thanks!
That salad looks beautiful! I am not a fan of arugula, though, my hubby and I find them bitter. Hehe!
You can substitute lettuce na lang for the arugula. heehee
A meal to look forward to. Looks very tatsty. Thanks for sharing!
you’re welcome.
I love your food posts, especially the healthy ones. Thanks fir sharing.
★★★★
Thanks Juvy Ann!
This is an interesting combination! May I ask for the recipe of the baked salmon? 🙂 We love salmon. I have yet to find a good recipe though for baking it.
Will share a salmon recipe on my next post.
Thanks for sharing this! My husband and I have been eating more and more veggies and meat and less rice to our diet. Very timely post, I needed some new ideas for what to prepare next time 🙂
You’re welcome Lique!
Oh my gosh. That looks soon good! I stared at your salad photo for a good minute before realizing there was more of the post to read! Haha!
heehee. Thanks Monica!
Gaaah all my favourite things in one salad! I imagine it to be very flavourful and refreshing. Yum!
Thanks Maan!
I love the idea of making apple cranberry cashew salad, this looks like a great mix of ingredients to enjoy!
It is. the flavors are wonderful!
I’m starting a new love affair with salads and this looks like an interesting pairing. I can just imagine the texture! And that baked salmon. Man, I got hungry haha 😀
heehee.. Make it na mommy!
That salad looks so good! I love all of the ingredients you used, so I’m going to have to put them on my shopping list to make this!
Thanks Christy. I’m sure you’ll love it.
That salad looks absolutely amazing. I need more salad recipes for the hot summer months. Looks so delicious.
★★★★★
Thanks Chrishelle!
Your Apple Cranberry Cashew Salad looks tempting! It’s a perfect complement to your Baked Salmon!
Yes it is. Thanks Tetcha!
It looks sooo good! I’m heading to the grocery store to make this salad tomorrow! Yummy!
Thanks Claudia!
I love fruit in my salads, especially for summertime! This sounds like a delicious combination
I’m sure this is perfect for you.
This would make a great delicious light lunch option I can take with me to work. I really like the sweet & tartness that cranberries offer.
This looks delicious! I love cranberries and apples, so I am sure I will love this salad.
★★★★★
I am so sure you will!
This salad is one of my favorites and I love feta and apples. I usually use walnuts or pecans in salads but cashews add a whole new taste profile. Now I need to go to the store so I can make this.
★★★★★
You’ll love this too, I bet!
This Apple Cranberry Cashew Salad looks so good!!! It was even paired with a Baked Salmon which looks delicious as well.
★★★★★
Thanks Leira!
That salad looks so healthy. Unfortunately, we aren’t into salads. I still prefer cooked greens. I do love taco salad though. Haha.
Thanks MaeMeMimommy!
Interesting salad, bookmarking this for our next meal!
Oh you’ll love it.
That looks so tasty! I love that people are using fruit more in salads. I think it completes the salad and actually helps with your dietary needs including a lot of food groups at once.
True! Thanks Heather!
I’m not really fond of green apples but the salad looks delish! And that salmon … yum!
Thanks Edel!
Oh dear, I wish I could have a taste of the baked salmon. It looks so delish! I really am starving at this hour of the night! Haha
heehee. Thanks Michelle!
This is a delicious (and gorgeous) looking salad! Yum! I am always looking for great salad recipes. Thanks!
★★★★★
you’re welcome Amy!
Love dishes that are so appealing to the eye and healthy for the gut!!!! I will be trying this soon!
Thanks Jessica!
Yum! I love the ingredients in this salad. It looks like the perfect light and healthy dish for Summer! Can’t wait to try it
Thank you Ashley!
Yummy! We use cashews in our cooking a lot, but I’ve never made salads with it. I really like adding apples and cashews together!
Then you’ll love this salad!
oh that salad looks delish, you had me at arugala, lol….love that combo with cheese and cranberries and nuts. yuuuummmyyyy
★★★★★
Thanks Mike!
Wow! I love this. I am really thankful for this post because I am looking for a new taste of salad. Salad is our favorite and I really wanna try something new. More delicious salad recipe please?
★★★★★
Alright. I’ll put up more salad recipes!
Omg this salad looks absolutely amazing!!!!!! I must pin so I can give it a try!!!!! Yum!
Thanks CourtneyLynne!
wow! It looks really yummy! I always get hungry every time I visit this site! lol.
Thanks Nilyn!
Healthy food, I love to eats salad but I am so picky with the veggies.
What veggies are you not fond of eating?
This has to be on my list of salad recipes! I really like that you combined apple and cranberries, this will make it more refreshing and nutritious.
Thanks Elizabeth!
Wow! I’ll try this one time! My hubby loves salad for dinner. And Cashew? He’ll die! Thanks for sharing this! Love your recipes by the way!
Thanks Arlene!
They look so yummy and healthy too!
I hope your little one gets well soon…
Thanks Kristine!
While this looks great, I can’t eat it since I’m allergic to apples and nuts. 🙁
Aww, that’s too bad.
It looks really fresh, healthy and delicious. Love apples 🙂
Thanks Mark!
That’s a really yummy and tasty salad that you made.
Thank you Dominique!
This is perfect for us. I will check all the ingredients if we can afford it, hehe.
Of course you can naman..
So much flavours and textures in here. happiness in each bite
★★★★★